-
The bit-depth & type of an image determine what pixel values it can contain
-
An image with a higher bit-depth can (potentially) contain more information
-
For acquisition, most images have the type unsigned integer
-
For processing, it is often better to use floating point types
-
Attempting to store values outside the range permitted by the type & bit-depth leads to clipping
Types & bit-depths
Possible & impossible pixels
As described in Images & Pixels, each pixel has a numerical value – but a pixel cannot typically have just any numerical value it likes. Instead, it works under the constraints of the image type and bit-depth. Ultimately the pixels are stored in some binary format: a series of bits (binary digits), i.e. ones and zeros. The bit-depth determines how many of these ones and zeros are available for the storage of each pixel. The type determines how these bits are interpreted.
Representing numbers with bits
Suppose you are developing a code to store numbers, but in which you are only allowed to write ones and zeros. If you are only allowed a single one or zero, then you can only actually represent two different numbers. Clearly, the more ones and zeros you are allowed, the more unique combinations you can have – and therefore the more different numbers you can represent in your code.
A 4-bit example
The encoding of pixel values in binary digits involves precisely this phenomenon. If we first assume we have a 4 bits, i.e. 4 zeros and ones available for each pixel, then these 4 bits can be combined in 16 different ways:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Here, the number after the arrow shows how each sequence of bits could be interpreted. We do not have to interpret these particular combinations as the integers from 0–15, but it is common to do so – this is how binary digits are understood using an unsigned integer type. But we could also easily decide to devote one of the bits to giving a sign (positive or negative), in which case we could store numbers in the range -8 – +7 instead, while still using precisely the same bit combinations. This would be a signed integer type.
Of course, in principle there are infinite other variations of how we interpret our 4-bit binary sequences (integers in the range -7 – +8, even numbers between 39 to 73, the first 16 prime numbers etc.), but the ranges I’ve given are the most normal.
In any case, the main point is that knowing the type of an image is essential to be able to decipher the values of its pixels from how they are stored in binary.
Increasing bit depths
So with 4 bits per pixel, we can only represent 16 unique values. Each time we include another bit, we double the number of values we can represent.
Computers tend to work with groups of 8 bits, with each group known as 1 byte. Microscopes that acquire 8-bit images are still common, and these permit 28 = 256 different pixel values, which, understood as unsigned integers, fall in the range 0–255. The next step up is a 16-bit image, which can contain 216 = 65536 values: a dramatic improvement (0–65535). Of course, because twice as many bits are needed for each pixel in the 16-bit image when compared to the 8-bit image, twice as much storage space is required - leading to larger file sizes.
Floating point types
Although the images we acquire are normally composed of unsigned integers, we will later explore the immense benefits of processing operations such as averaging or subtracting pixel values, in which case the resulting pixels may be negative or contain fractional parts. Floating point type images make it possible to store these new, not-necessarily-integer values in an efficient way.
Floating point pixels have variable precision depending upon whether or not they are representing very small or very large numbers. Representing a number in binary using floating point is analogous to writing it out in standard form, i.e. something like 3.14 × 108. In this case, we have managed to represent 314000000 using only 4 digits: 314 and 8 (the 10 is already known in advance). In the binary case, the form is more properly something like ± 2M × N: we have one bit devoted to the sign, a fixed number of additional bits for the exponent M, and the rest to the main number N (called the fraction).
A 32-bit floating point number typically uses 8 bits for the exponent and 23 bits for the fraction, allowing us to store a very wide range of positive and negative numbers. A 64-bit floating point number uses 11 bits for the exponent and 52 for the fraction, thereby allowing both an even wider range and greater precision. But again these require more storage space than 8- and 16-bit images.
Limitations of bits
The main point of Images & Pixels is that we need to keep control of our pixel values so that our final analysis is justifiable. In this regard, there are two main bit-related things that can go wrong when trying to store a pixel value in an image:
-
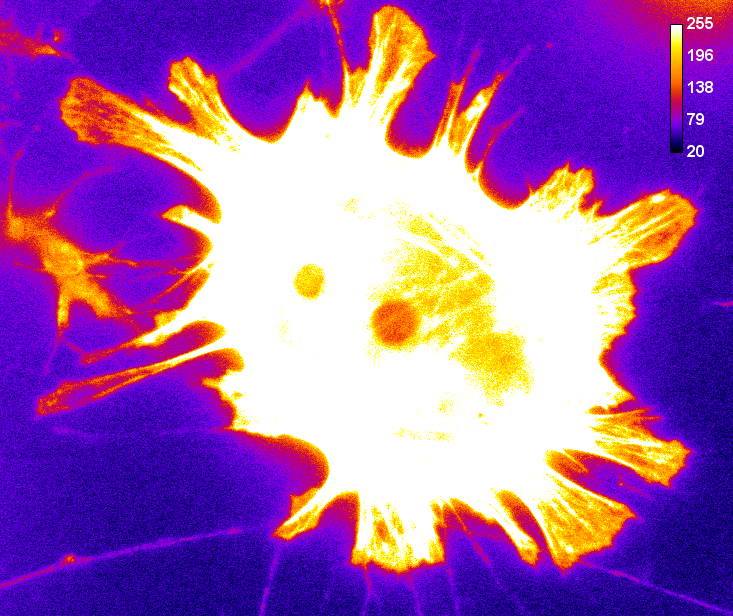
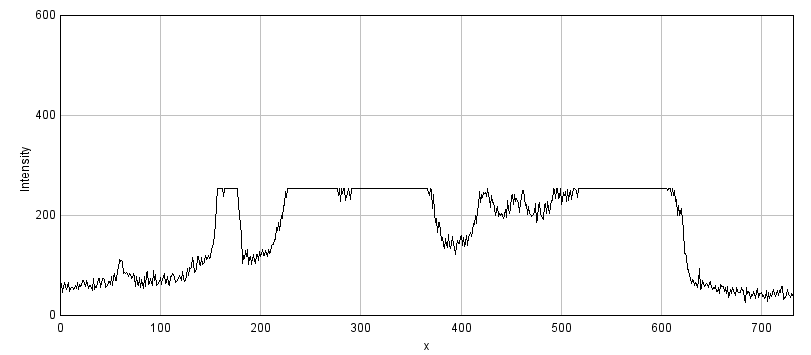
Clipping: We try to store a number outside the range supported, so that the closest valid value is stored instead, e.g. trying to put -10 and 500 into an 8-bit unsigned integer will result in the values 0 and 255 being stored instead.
-
Rounding: We try to store a number that cannot be represented exactly, and so it must be rounded to the closest possible value, e.g. trying to put 6.4 in an 8-bit unsigned integer image will result in 6 being stored instead.
Data clipping
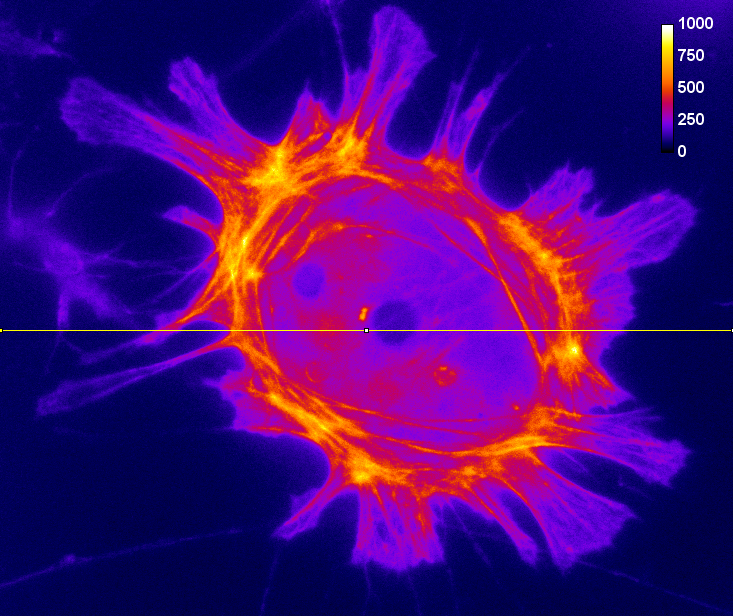
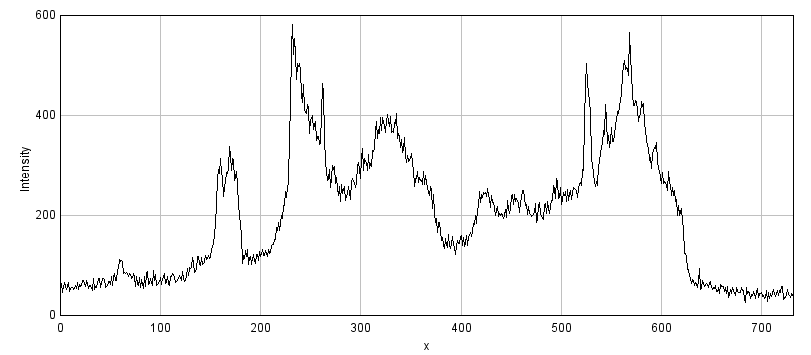
Of the two problems, clipping is usually the more serious, as shown in Figure 1. A clipped image contains pixels with values equal to the maximum or minimum supported by that bit-depth, and it is no longer possible to tell what values those pixels should have. The information is irretrievably lost.
Clipping can already occur during image acquisition, where it may be called saturation. In fluorescence microscopy, it depends upon three main factors:
-
The amount of light being emitted. Because pixel values depend upon how much light is detected, a sample emitting very little light is less likely to require the ability to store very large values. Although it still might because of…
-
The gain of the microscope. Quantifying very tiny amounts of light accurately has practical difficulties. A microscope’s gain effectively amplifies the amount of detected light to help overcome this before turning it into a pixel value (see Microscopes & detectors). However, if the gain is too high, even a small number of detected photons could end up being over-amplified until clipping occurs.
-
The offset of the microscope. This effectively acts as a constant being added to every pixel. If this is too high, or negative, it can also push the pixels outside the permissible range.
If clipping occurs, we no longer know what is happening in the brightest or darkest parts of the image – which can thwart any later analysis. Therefore during image acquisition, any gain and offset controls should be adjusted as necessary to make sure clipping is avoided.
Rounding errors
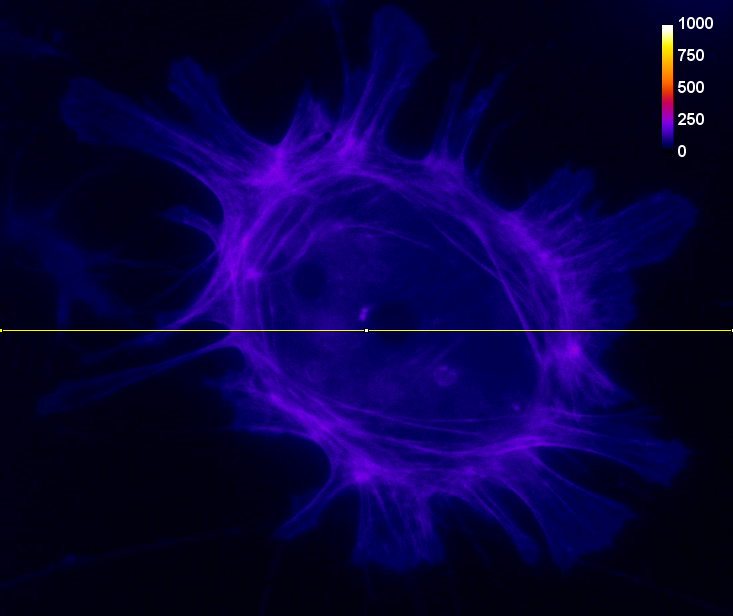
Rounding is a more subtle problem than clipping. Again it is relevant as early as acquisition. For example, suppose you are acquiring an image in which there really are 1000 distinct and quantifiable levels of light being emitted from different parts of a sample. These could not possibly be given different pixel values within an 8-bit image, but could normally be fit into a 16-bit or 32-bit image with lots of room to spare. If our image is 8-bit, and we want to avoid clipping, then we would need to scale the original photon counts down first – resulting in pixels with different photon counts being rounded to have the same values, and their original differences being lost.
Nevertheless, rounding errors during acquisition are usually small. Rounding can be a bigger problem when it comes to processing operations like filtering, which often involve computing averages over many pixels (see Filters). But, fortunately, at this post-acquisition stage we can convert our data to floating point and then get fractions if we need them.
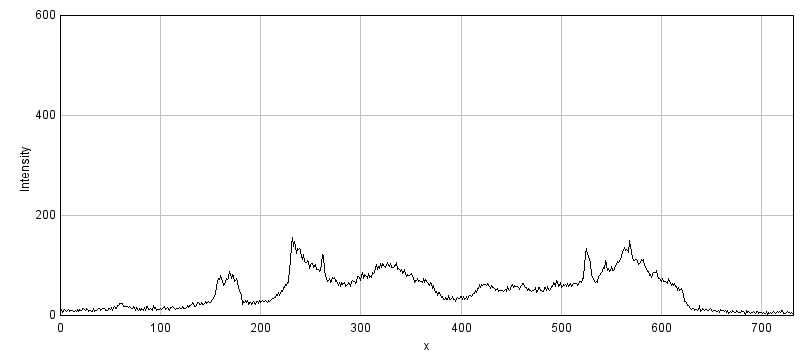
More bits are better… usually
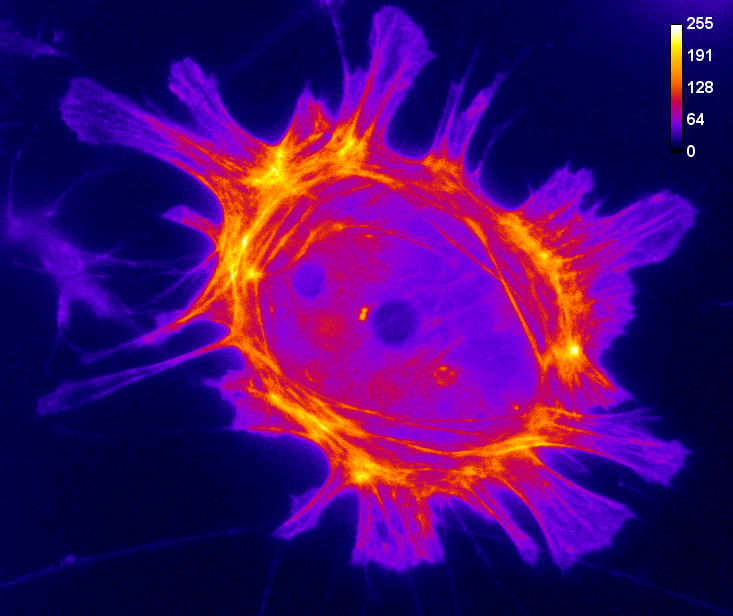
From considering both clipping and rounding, the simple rule of bit-depths emerges: if you want the maximum information and precision in your images, more bits are better. This is depicted in Figure 2. Therefore, when given the option of acquiring a 16-bit or 8-bit image, most of the time you should opt for the former.
Converting images in ImageJ
For all that, sometimes it is necessary to convert an image type or bit-depth, and then caution is advised.
This conversion could even sometimes be required against your better judgement, but you have little choice because a particular command or plugin that you need has only been written for specific types of image. And while this could be a rare event, the process is unintuitive enough to require special attention.
Conversions are applied in ImageJ using the commands in the
submenu. The top three options are 8-bit (unsigned
integer), 16-bit (unsigned integer) and 32-bit (floating point),
which correspond to the types currently supported[1].
In general, increasing the bit-depth of an image should not change the
pixel values: higher bit-depths can store all the values that lower
bit-depths can store. But going backwards that is not the case, and when
decreasing bit-depths one of two things can happen depending upon
whether the option Scale When Converting under
is checked or not.
-
Scale When Convertingis not checked: pixels are simply given the closest valid value within the new bit depth, i.e. there is clipping and rounding as needed. -
Scale When Convertingis checked: a constant is added or subtracted, then pixels are further divided by another constant before being assigned to the nearest valid value within the new bit depth. Only then is clipping or rounding applied if it is still needed.
Perhaps surprisingly, the constants involved in scaling are determined
from the Minimum and Maximum in the current Brightness/Contrast…
settings: the Minimum is subtracted, and the result is divided by
Maximum - Minimum. Any pixel value that was lower than Minimum or
higher than Maximum ends up being clipped. Consequently, converting
to a lower bit-depth with scaling can lead to different results
depending upon what the brightness and contrast settings were.