Manipulating individual pixels

Chapter outline

  • Point operations are mathematical operations applied to individual pixel values

  • They can be applied using a single image, an image and a constant, or two images of the same size

  • Some point operations improve image appearance by changing the relationships between pixel values

Introduction

A step used to process an image in some way is called an operation, and the simplest examples are point operations. These act on individual pixels, changing each in a way that depends upon its own value, but not upon where it is or the values of other pixels. While not immediately very glamorous, point operations often have indispensable roles in more interesting contexts – and so it is essential to know where to find them and how they are used.

Point operations using a single image

Arithmetic

The Process ▸ Math submenu is full of useful things to do with pixel values. At the top of the list come the arithmetic operations: Add…​, Subtract…​, Multiply…​ and Divide…​. These might be used to subtract background (extremely important when quantifying intensities; see Simulating image formation) or scale the pixels of different images into similar ranges (e.g. if the exposure time for one image was twice that of the other, the pixel values should be divided by two to make them more comparable) – and ought to mostly behave as you expect.

Question

Suppose you add a constant to every pixel in the image. Why might subtracting the same constant from the result not give you back the image you started with?

Answer

If you add a constant that pushes pixel values outside the range supported by the bit-depth (e.g. 0–255 for 8-bit), then the result is clipped to the closest possible value. Subtracting the constant again does not restore the original value. Note that this is less likely to occur with a 32-bit image.

Image inversion

Inverting an image (Edit ▸ Invert) effectively involves 'flipping' the intensities: making the higher values lower, and the lower values higher. In the case of 8-bit images, inverted pixel values can be easily computed simply by subtracting the original values from the maximum possible – i.e. from 255. Although this would work in principle for 16-bit images as well, it could have the slightly uncomfortable effect of making an image containing only small values suddenly now only contain huge ones.

Why is inversion useful?

Suppose you have a good strategy designed to detect bright structures, but your images contain dark structures. Simply invert your images first, then the structures become bright.

Practical

Edit ▸ Invert works differently when applied to different image types. Like in the 8-bit case, pixel values are always subtracted from some 'maximum' – your challenge is to work out how this maximum is determined for 16 and 32-bit images in ImageJ.

(Note that the methods used for 16 and 32-bit images are not even the same as one another.)

Answer

At the time of writing, to invert a 16-bit image, pixel are subtracted from the maximum value within the original image. This is also true for stacks: the maximum value in the entire stack is found.

For 32-bit image inversion, the pixels are subtracted from the display maximum, i.e. whatever maximum is set in the Brightness/Contrast…​ dialog box. Consequently, inverting a 32-bit image can give different results each time it is applied if the contrast settings are not kept the same!

One way to improve predictability when inverting a 32-bit image is simply to multiply each pixel by -1 instead of using the Invert command – although this would not be a good strategy for 8 or 16-bit images.

hanger on.png
A: Original image
hanger on invert.png
B: Inverted image
hanger on invert.png
C: Inverted LUT
hanger on.png
D: Inverted image + inverted LUT

Figure 1: The effect of image and LUT inversion on a depiction of two young lovers, spotted on Gaisbergstraße displaying the virtues of invention and tolerance.

Inverting LUTs

Beware! You can also invert the colors used for display with Image ▸ Lookup Tables ▸ Invert LUT – which looks the same as if the image is inverted, but does not change the pixel values (Figure 1)!

Moreover, whether the LUT is inverted is saved inside TIFF files – and so you could potentially open an image and find its LUT was inverted before you even started to do anything, and thereby misjudge whether structures are really brighter or darker than everything else. See File ▸ Open Samples ▸ Blobs for an example of this.

Nonlinear contrast enhancement

With arithmetic operations we change the pixel values, usefully or otherwise, but (assuming we have not fallen into the trap alluded to in a previous question) we have done so in a linear way. At most it would take another multiplication and/or addition to get us back to where we were. Because a similar relationship between pixel values exists, we could also adjust the Brightness/Contrast…​ so that it does not look like we have done anything at all.

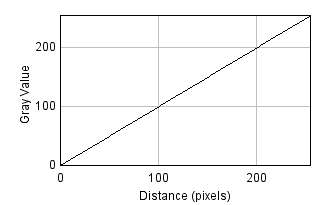
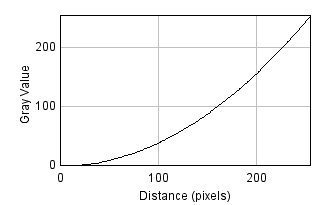
Nonlinear point operations differ in that they affect relative values differently depending upon what they were in the first place (Figure 2). This turns out to be very useful for displaying images with high dynamic ranges – that is, a big difference between the largest and smallest pixel values (e.g. Figure 3). Using the Brightness/Contrast…​ tool (which assigns LUT colors linearly to all the pixel values between the minimum and maximum chosen) it might not be possible to find settings that assign enough different colors to the brightest and darkest regions simultaneously for all the interesting details to be made visible.

nonlinear ramp.png
nonlinear log.png
nonlinear gamma 05.png
nonlinear gamma 2.png
nonlinear ramp plot.png
A: Original (linear)
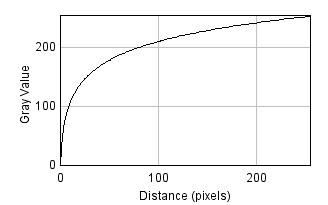
nonlinear log plot.png
B: Log
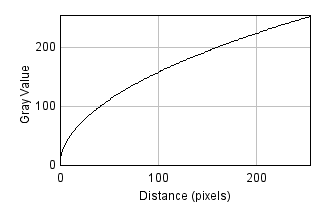
nonlinear gamma 05 plot.png
C: Gamma = 0.5
nonlinear gamma 2 plot.png
D: Gamma = 2.0

Figure 2: Nonlinear transforms applied to a simple 'ramp' image, consisting of linearly increasing pixel values. Replacing each pixel with its log or gamma-adjusted value has the effect of compressing either the lower or higher intensities closer together to free up more gray levels for the others.

The Gamma…​ or Log…​ commands within the Process ▸ Math submenu offer one type of solution. The former means that every pixel with a value p is replaced by pγ, where γ is some constant of your choosing. The latter simply replaces pixel values with their natural logarithm. Examples of these are shown in Figure 3. Some extra (linear) rescaling is applied internally by ImageJ when using gamma and log commands, since otherwise the resulting values might fall out of the range supported by the bit-depth.

spooked orig.png
A: Original image
spooked contrast.png
B: Linear contrast
spooked gamma 03.png
C: Gamma adjusted
spooked log.png
D: Log transform

Figure 3: The application of nonlinear contrast enhancement to an image with a wide range of values. (Top row) In the original image, it is not possible to see details in both the foreground and background simultaneously. (Bottom row) Several examples of nonlinear techniques that make details visible throughout the image.

Practical

Explore the use of the nonlinear transforms in the ImageJ submenu Process ▸ Math for enhancing the contrast of any image (possibly Spooked_16-bit.tif). In particular, notice how the effects change depending upon whether γ < 1 or not.

Avoiding manipulation (important!)

When creating figures for publication, changing the contrast in some linear manner – i.e. just by scaling using the Brightness/Contrast…​ tool – is normally considered fine (assuming that it has not been done mischievously to make some inconvenient, research-undermining details impossible to discern). But if any nonlinear operations are used, these should always be noted in the figure legend! This is because, although nonlinear operations can be very helpful when used with care, they can also easily mislead – exaggerating or underplaying differences in brightness.

Point operations involving multiple images

Instead of applying arithmetic using an image and a constant, we could also use two images of the same size. These can readily be added, subtracted, multiplied or divided by applying the operations to the corresponding pixels.

The command to do this is found under Process ▸ Image Calculator…​. But beware of the bit-depth! If any of the original images are 8 or 16-bit, then the result might require clipping or rounding, in which case selecting the option to create a 32-bit (float) result may be necessary to get the expected output.

The image calculator

Uses of the image calculator include:

  • subtracting varying backgrounds

  • comparing images

  • computing intensity ratios

  • masking out regions

    • and much more…​

Question

In the two 32-bit images shown here, white pixels have values of one and black pixels have values of zero (gray pixels have values somewhere in between).

mask orig.png
mask bacteria.png

What would be the result of multiplying the images together? And what would be the result of dividing the left image by the right image?

Answer

Multiplying the images effectively results in everything outside the white region in the right image being removed from the left image (i.e. set to zero).

mask result.png

Dividing has a similar effect, except that instead of becoming zero the masked-out pixels will take one of three results, depending upon the original pixel’s value in the left image:

  • if it was positive, the result is

  • if it was negative, the result is

  • if it was zero, the result is NaN ('not a number' – indicating 0/0 is undefined)

These are special values that can be contained in floating point images, but not images with integer types.

Practical

With the help of the Image Calculator, confirm which two of the images Same_1.tif, Same_2.tif and Same_3.tif are identical in terms of pixel values, and which is different.

Answer

My preferred way to check this is to subtract the images from one another, making sure that the result is 32-bit (in case there are negative values). Doing this should reveal something hidden in the image Same_2.tif. Note that the contrast settings differ between Same_1.tif and Same_3.tif, so they may look different.

(Note that the calculator’s Difference or Divide commands could also be used. XOR would work as well, but its output is harder to interpret since it involves comparing individual bits used to store each pixel value and gives an output where all matching bits are 0 and all non-matching bits are 1. When converted back into actual decimal values and then to colors for us to look at, this can appear strange. But at least if the resulting image is not completely black then we know that the original input images were not identical.)

Modelling image formation: Adding noise

Fluorescence images are invariably noisy. The noise appears as a graininess throughout the image, which can be seen as arising from a random noise value (positive or negative) being added to every pixel. This is equivalent to adding a separate 'noise image' to the non-existent cleaner image that we would prefer to have recorded. If we knew the pixels in the noise image then we could simply subtract it to get the clean result – but, in practice, their randomness means that we do not.

adding noise.png

Nevertheless, even the idea of a noise image being added is extremely useful. We can use it to create simulations in which the noise behaves statistically just like real noise, and add it to clean images. Using these simulations we can figure out things like how processing steps or changes during acquisition will affect or reduce the noise, or how sensitive our measurement strategies are to changes in image quality (see Filters, Noise and Simulating image formation).

results matching ""

    No results matching ""