In image processing literature, interesting image structures are frequently called objects (or sometimes connected components), and the often troublesome process of detecting them is image segmentation.

Most of the techniques described in the following chapters can be strung together in an effort to segment an image accurately. If successful, the result may be a binary image, in which each pixel can only have one of two values to indicate whether it is part of an object or not, or a labeled image, in which all pixels that are part of the same object have the same, unique value. It is common to concentrate first on producing a binary image, and then create a labeled image only if necessary by identifying distinct clusters of object pixels and assigning the labels to these.

The puzzle of global thresholding is how to define the thresholds sensibly. If you open File ▸ Open Samples ▸ HeLa Cells and split the channels (Image ▸ Color ▸ Split Channels), you can use Threshold…​ to interactively try out different possibilities for each channel. You should soon notice the danger in this: the results (especially in the red or green channels) can be very sensitive to the threshold you choose. Low thresholds tend to detect more structures, and also to make them bigger – until the point at which the structures merge, and then there are fewer detected again (Figure 1).

In other words, you can sometimes use manual thresholds to get more or less whatever result you want – which could completely alter the interpretation of the data. For the upstanding scientist who finds this situation disconcerting, ImageJ therefore offers a number of automated threshold determination methods in a drop-down list in the Threshold…​ tool. These are described at http://imagej.net/Auto_Threshold, often with references to the original published papers upon which they are based. Fiji’s Image ▸ Adjust ▸ Auto Threshold command provides additional options, including the ability to apply all the thresholds and see which one appears to provide the best results.

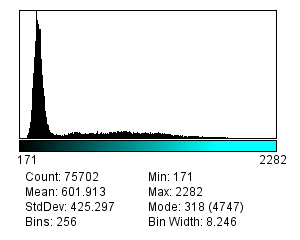
There is no always-applicable strategy to determine a threshold; images vary too much. However, by its nature, thresholding assumes that there are two classes of pixel in the image – those that belong to interesting objects, and those that do not – and pixels in each class have different intensity values^[2]. Whenever values are significant, but their exact location in the image is either unknown or unimportant, this information is neatly summarized within the image’s histogram. Therefore ImageJ’s methods to find thresholds do not work on the images directly, but rather on their histograms – which is considerably simpler.

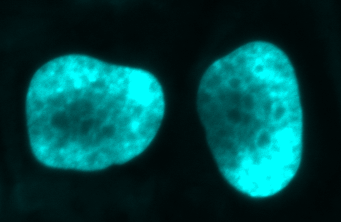
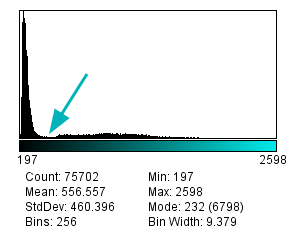
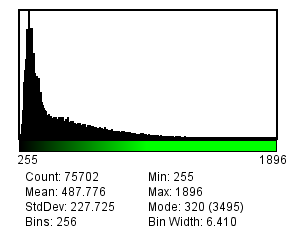
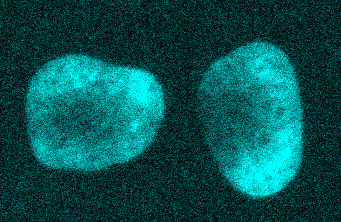
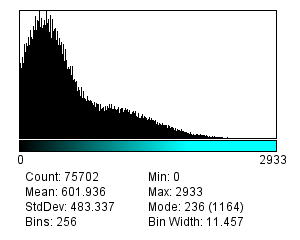
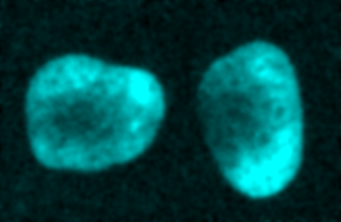
A justification for this can be seen in Figure 2. Looking at the image, the two nuclei are obvious: they clearly have higher values than the background (A). However, looking at the histogram alone (B) we could already have inferred that there was a class of background pixels (the tall peak on the left) and a class of 'other', clearly distinct pixels (the much shallower peak on the right). By choosing a threshold between these two peaks – somewhere around 400 – the nuclei can be cleanly separated (C). Choosing a threshold much higher or lower than this yields less impressive results (D).

Figure 3 gives a more challenging example. In the image itself the structures are not very clearly defined, and in many cases it is not obvious whether we would want to consider any particular pixel as 'bright enough' for detection or not (A). The histogram also depicts this uncertainty; there is a smoother transition between the background peak and the foreground (B). The results of applying two different automated thresholds are shown, (C) and (D). Both are in some sense justifiable, and deciding which is the most appropriate would require a deeper understanding of what the image contains and what is to be analyzed.

Noise is one problem that affects thresholds, especially in live cell imaging. The top half of Figure 4 reproduces the nuclei from Figure 2, but with extra noise added to simulate less than ideal imaging conditions. Although the nuclei are still clearly visible in the image (A), the two classes of pixel previously easy to separate in the histogram have now merged together (B). The triangle threshold method, which had performed well before, now gives less attractive results (C), because the noise has caused the ranges of background and nuclei pixels to overlap. However, applying a Gaussian filter smooths the image, thereby reducing much of the random noise (see Filters), which results in a histogram dramatically more similar to that in the original, (almost) noise-free image, and the threshold is again quite successful (F).

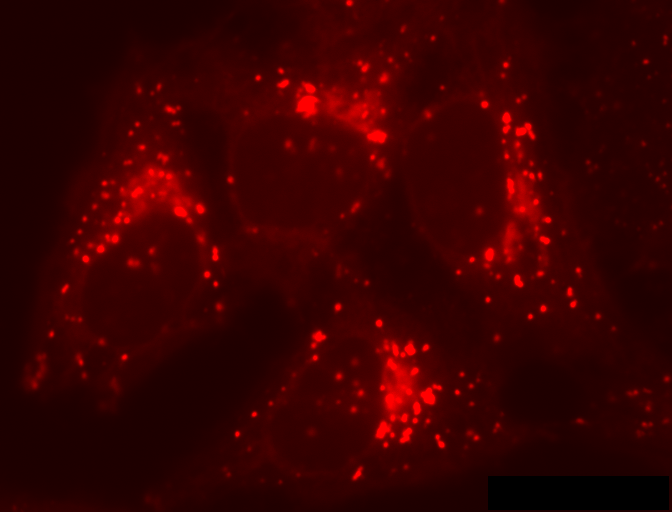
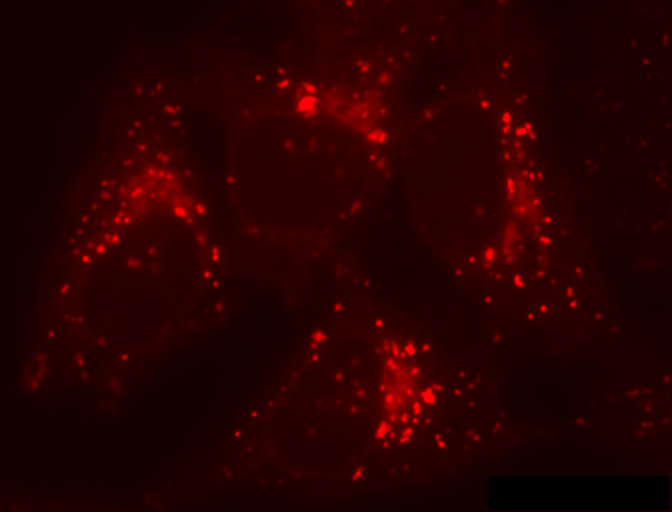
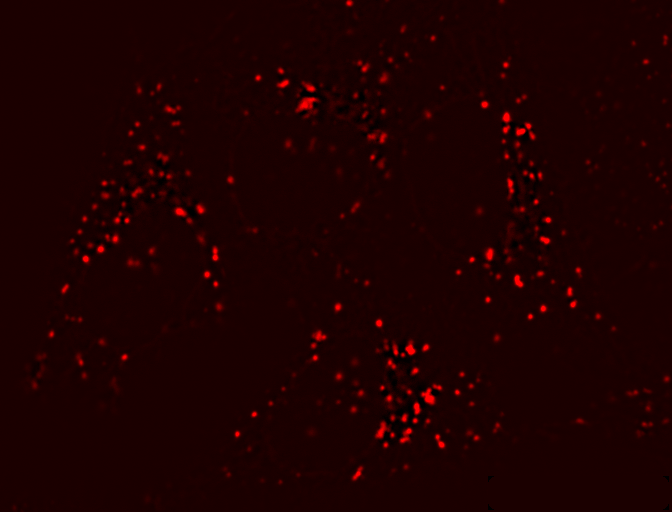
Another common problem is that structures that should be detected appear on top of a background that itself varies in brightness. For example, in the red channel of HeLa cells there is no single global threshold capable of identifying and separating all the 'spot-like' structures; any choice will miss many of the spots because a threshold high enough to avoid the background will also be too high to catch all the spots occurring in the darker regions (Figure 5a–c).

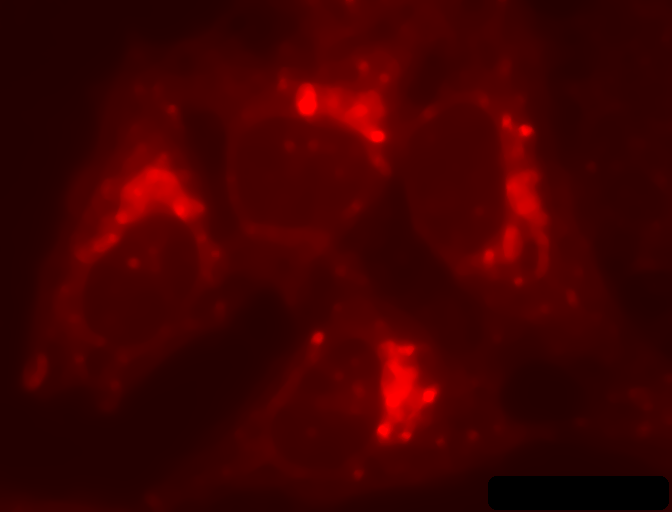
In such cases it would be better if we could define different thresholds for different parts of the image: a local threshold. A few methods to do this are implemented in Fiji’s Image ▸ Adjust ▸ Auto Local Threshold, and described at http://imagej.net/Auto_Local_Threshold. However, if these are insufficient it is easy to implement our own local thresholding and get more control over the result if we think of the problem from a slightly different angle. Suppose we had a second image that contained values equal to the thresholds want to apply, and which could be different for every pixel. If we simply subtract this second image from the first, we can then apply a global threshold to detect what we want.

The difficult part is creating the second image, but again filters come in useful. One option is a median filter, which effectively moves through every pixel in the image, ranks the nearby pixels in order of value, and chooses the middle one – thereby removing anything much brighter or much darker than its surroundings (D). Subtracting the median-filtered image from the original gives a result to which a global threshold can be usefully applied (E).

Although not obviously integral to the idea of thresholding, bit-depths and image types are relevant in two main ways.

The first appears when you click Apply in the Threshold…​ dialog box for a 32-bit image. This presents the option Set Background Pixels to NaN, which instead of making a binary image would give give an image in which the foreground pixels retain their original values, while background pixels are Not A Number. This is a special value that can only be stored in floating point images, which ImageJ ignores when making measurements later. It is therefore used to mask out regions.

The second way in which bit-depths and types matter is that histograms of images > 8-bit involve binning the data. For example, with a 32-bit image it would probably not make sense to create a histogram that has separate counts for all possible pixel values: in addition to counts for pixels with exact values 1 and 2, we would have thousands of counts for pixels with fractions in between (and most of these counts would be 0). Instead, the histogram is generated by dividing the total data range (maximum – minimum pixel values) into 256 separate bins with equal widths, and counting how many pixels have values falling into the range of each bin. It is therefore like a subtle conversion to 8-bit precision for the threshold calculation, but without actually changing the original data. The same type of conversion is used for 16-bit images – unless you use Fiji’s Image ▸ Adjust ▸ Auto Threshold command, which uses a full 16-bit histogram with 65536 bins.

Although binning effects can often be ignored, if the total range of pixel values in an image is very large then it is worth keeping in mind.

Once we have a binary image, the next step is to identify objects within it and measure them. In 2D, there are several options:

Analyze Particles…​ is the most automated and versatile option, making it possible to ignore regions that are particularly small or large, straight or round (using a Circularity metric). It can also output summary results and add ROIs for each region to the ROI Manager. With the Show: Count Masks option, it will generate a labeled image, in which each pixel has a unique integer value indicating the number of the object it is part of – or zero if it is in the background. With a suitably colorful LUT, this can create a helpful and cheerful display (Figure 6).

Although binary images can show the shapes of things to be measured, pixel intensity measurements made on a binary image are not very helpful. You could use the above techniques to make ROIs from binary images, then apply those to the original image to get meaningful measurements. However, it is possible to avoid this extra step by changing the Redirect to: option under Set Measurements…​. This allows you to measure ROIs or run Analyze Particles…​ with one image selected and used to define the regions, while redirecting your measurements to be made on a completely different image of your choice.

If you use this, just be sure to reset the Redirect to: option when you are done, to avoid accidentally measuring the wrong image for so long as it is open.