-
Filters can be used to reduce noise and/or enhance features, making detection & measurement much easier
-
Linear filters replace each pixel by a weighted sum of surrounding pixels
-
Nonlinear filters replace each pixel with the result of some other computation using surrounding pixels
-
Gaussian filters have various advantages that make them a good choice for many applications with fluorescence images
Filters
Introduction
Filters are phenomenally useful. Almost all interesting image analysis involves filtering of some sort at some stage. In fact, the analysis of a difficult image sometimes becomes trivial once a suitable filter has been applied to it. It is therefore no surprise that much of the image processing literature is devoted to the topic of designing and testing filters.
The basic idea of filtering here is that each pixel in an image is assigned a new value depending upon the values of other pixels within some defined region (the pixel’s neighborhood). Different filters work by applying different calculations to the neighborhood to get their output. Although the plethora of available filters can be intimidating at first, knowing only a few of the most useful is already a huge advantage.
This chapter begins by introducing several extremely common linear and nonlinear filters for image processing. It ends by considering in detail some techniques based on one particularly important linear filter.
Linear filtering
Linear filters replace each pixel with a linear combination ('sum of products') of other pixels. Therefore the only mathematical background they require is the ability to add and multiply.
Mean filters
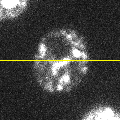
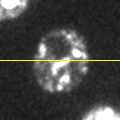
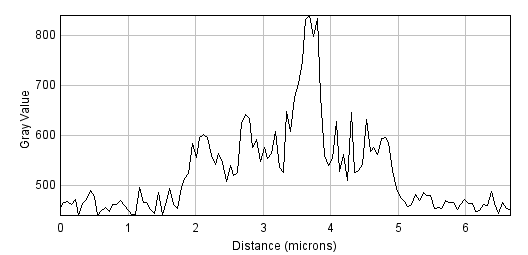
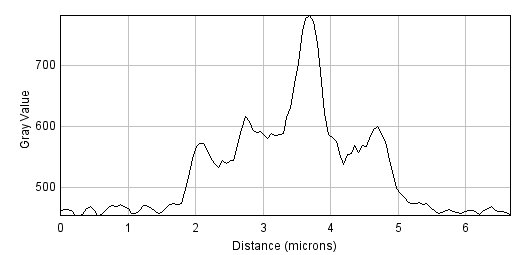
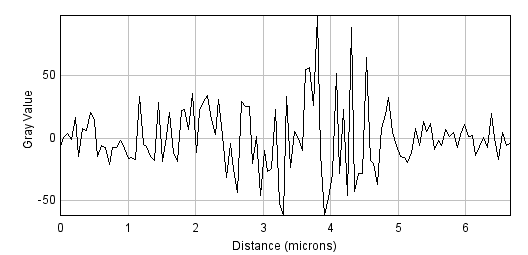
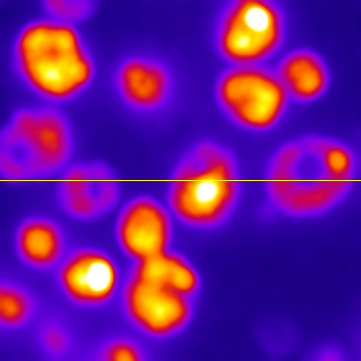
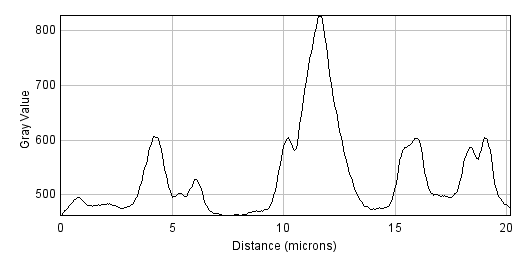
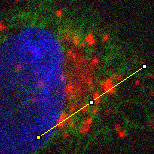
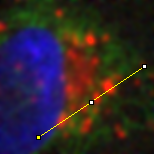
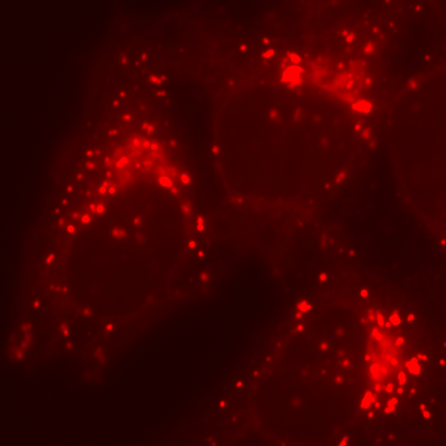
To begin, consider the somewhat noisy image of a yeast cell in Figure 1(A).
The noise can be seen in the random jumps in the fluorescence intensity profile shown. One way to improve this is to take each pixel, and simply replace its value with the mean (average) of itself and the 8 pixels immediately beside it (including diagonals). This 'averages out' much of this noisy variation, giving a result that is considerably smoother (B). Subtracting the smoothed image from the original shows that what has been removed consists of small positive and negative values, mostly (but not entirely) lacking in interesting structure (C).
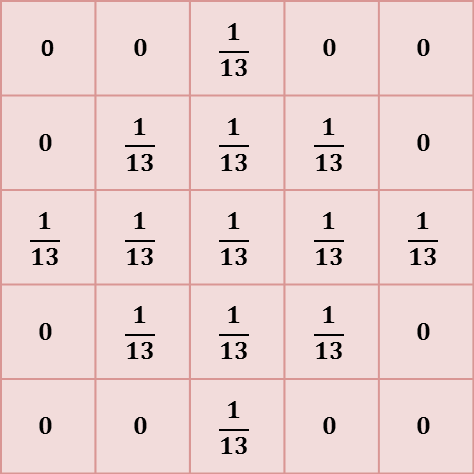
This smoothing is what a 3 × 3 mean filter[1] does. Each new pixel now depends upon the average of the values in a 3 × 3 pixel region: the noise is reduced, at a cost of only a little spatial information. The easiest way to apply this in ImageJ is through the command[2]. But this simple filter could be easily modified in at least two ways:
-
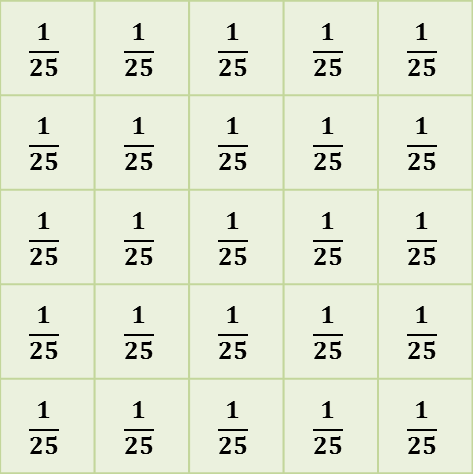
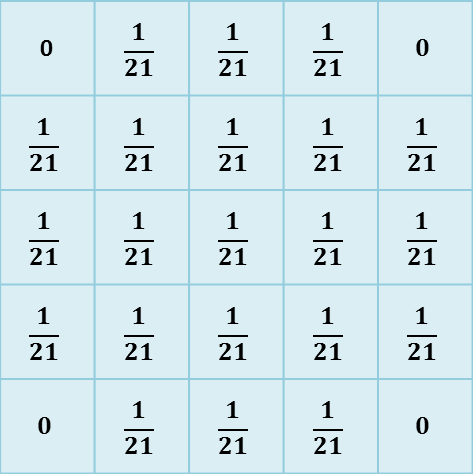
Its size could be increased. For example, instead of using just the pixels immediately adjacent to the one we are interested in, a 5 × 5 mean filter replaces each pixel by the average of a square containing 25 pixels, still centered on the main pixel of interest.
-
The average of the pixels in some other shape of region could be computed, not just an n × n square.
is ImageJ’s general command for mean
filtering. It uses approximately circular neighborhoods, and the
neighborhood size is adjusted by choosing a Radius value. The
Show Circular Masks command displays the neighborhoods used for
different values of Radius. If you happen to choose Radius = 1, you
get a 3 × 3 filter – and the same results as using
Smooth.
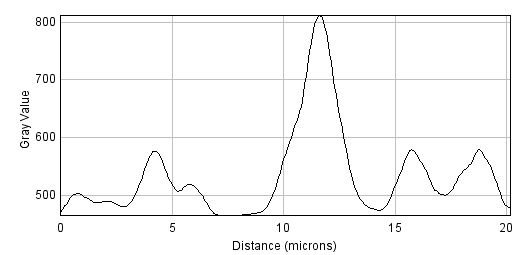
Figure 2 shows that as the radius increases, the image becomes increasingly smooth – losing detail along with noise. This causes the result to look blurry. If noise reduction is the primary goal, it is therefore best to avoid unnecessary blurring by using the smallest filter that gives acceptable results. More details on why mean filters reduce noise, and by how much, will be given in the chapter on Noise.
General linear filters
There are various ways to compute a mean of N different pixels. One is to add up all the values, then divide the result by N. Another is to multiply each value by 1/N, then add up the results. The second approach has the advantage that it is easy to modify to achieve a different outcome by changing the weights used to scale each pixel depending upon where it is. This is how a linear filter works in general, and mean filters are simply one specific example.
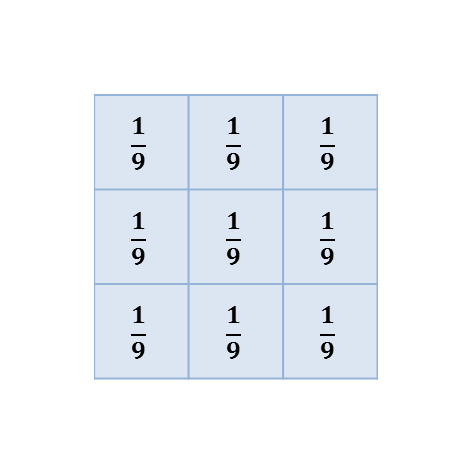
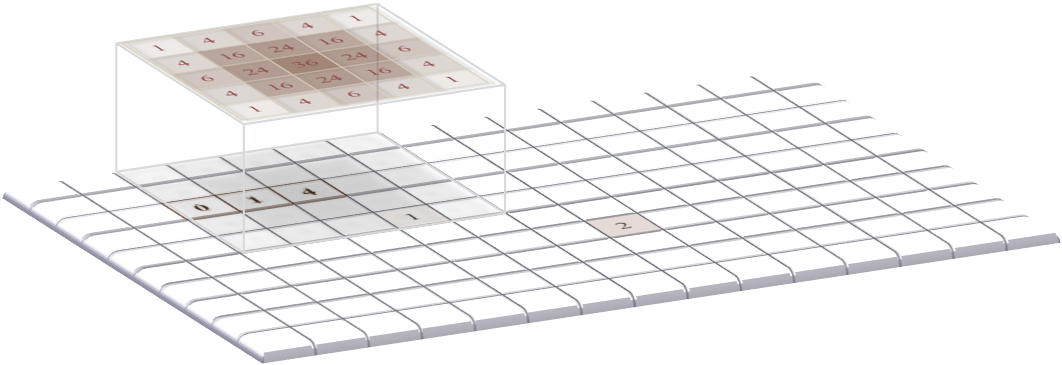
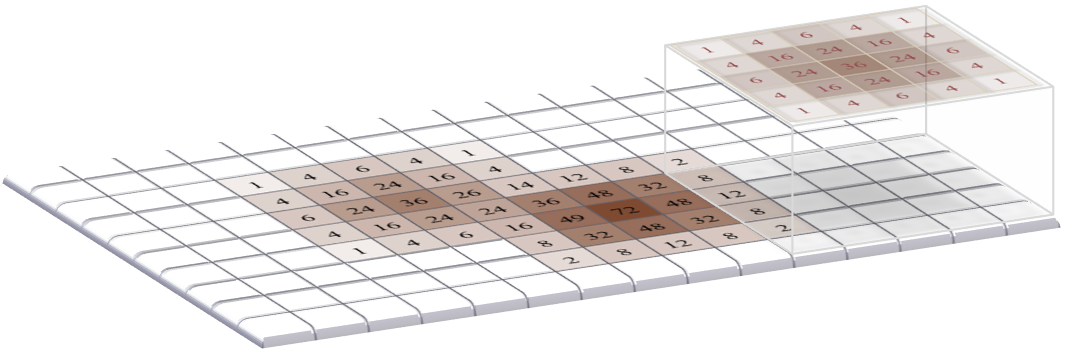
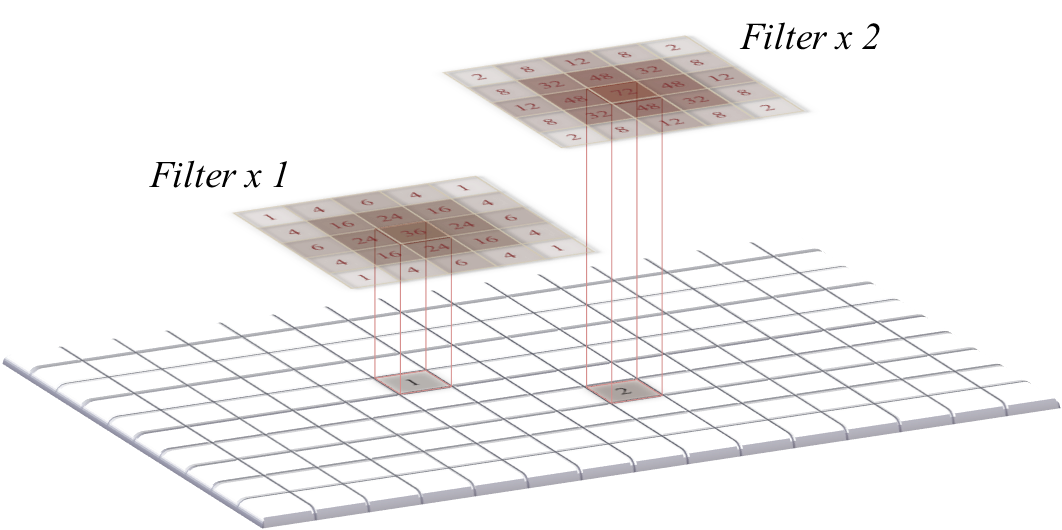
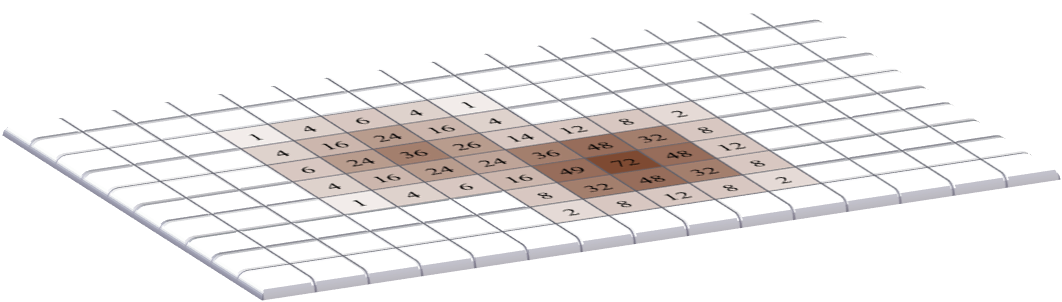
A linear filter is defined by a filter kernel (or filter mask). This resembles another (usually small and rectangular) image in which each pixel is known as a filter coefficient and these correspond to the the weights used for scaling. In the case of a mean filter, the coefficients are all the same (or zero, if the pixel is not part of the neighborhood), as shown in Figure 3. But different kernels can give radically different results, and be designed to have very specific properties.
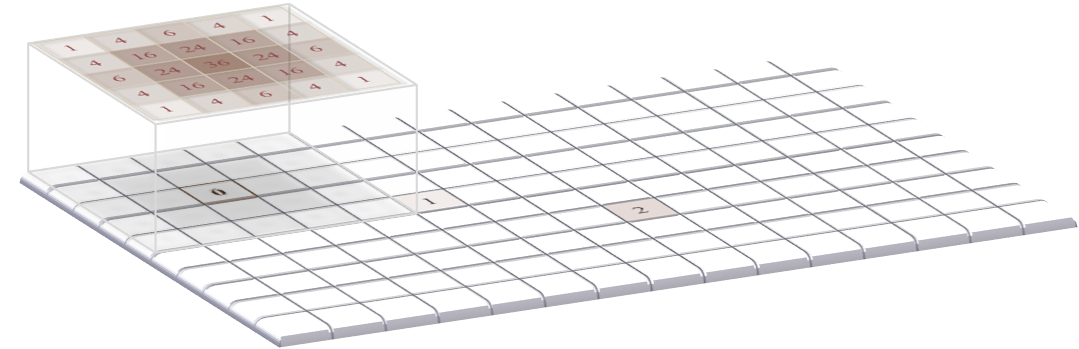
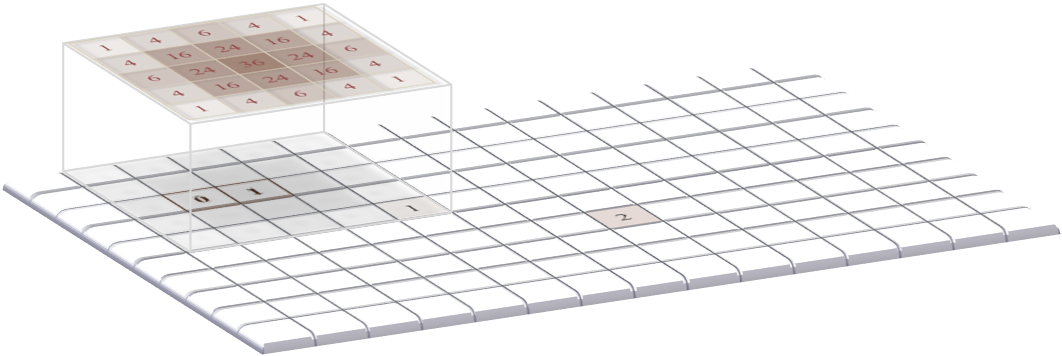
An algorithm to apply the filtering is shown in Figure 4.
Defining your own filters
The application of such filtering is often referred to as convolution,
and if you like you can go wild inventing your own filters using the
command. This allows you to choose
which specific coefficients the filter should have, arranged in rows and
columns. If you choose the Normalize Kernel option then the
coefficients are scaled so that they add to 1 (if possible), by dividing
by the sum of all the coefficients.
Gradient filters
Often, we want to detect structures in images that are distinguishable from the background because of their edges. So if we could detect the edges we would be making good progress. Because an edge is usually characterized by a relatively sharp transition in pixel values – i.e. by a steep increase or decrease in the profile across the image – gradient filters can be used to help.
A very simple gradient filter has the coefficients -1, 0, 1. Applied
to an image, this replaces every pixel with the difference between the
pixel to the right and the pixel to the left. The output is positive
whenever the fluorescence is increasing horizontally, negative when the
fluorescence is decreasing, and zero if the fluorescence is constant –
no matter what the original constant value was, so that flat areas are
zero in the gradient image irrespective of their original brightness. We
can also rotate the filter by 90 and get a vertical gradient image
(Figure 5).
Having two gradient images with positive and negative values can be somewhat hard to work with. If we square all the pixels in each, the values become positive. Then we can add both the horizontal and vertical images together to combine their information. If we compute the square root of the result, we get what is known as the gradient magnitude[3], which has high values around edges, and low values everywhere else. This is (almost) what is done by the command .
Convolution & correlation
Although linear filtering and convolution are terms that are often used synonymously, the former is a quite general term while the latter can be used in a somewhat more restricted sense. Specifically, for convolution the filter should be rotated by 180 before applying the algorithm of Figure 4. If the algorithm is applied without the rotation, the result is really a correlation. However, this distinction is not always kept in practice; convolution is the more common term, and often used in image processing literature whenever no rotation is applied. Fortunately, much of the time we use symmetric filters, in which case it makes absolutely no difference which method is used. But for gradient filters, for example, it is good to be aware that the sign out the output (i.e. positive or negative) would be affected.
Nonlinear filters
Linear filters involve taking neighborhoods of pixels, scaling them by specified constants, and adding the results to get new pixel values. Nonlinear filters also make use of neighborhoods of pixels, but with different calculations to obtain the output. Here we will consider one especially important family of nonlinear filters.
Rank filters
Rank filters effectively sort the values of all the neighboring pixels in ascending order, and then choose the output based upon this ordered list. The most common example is the median filter, in which the pixel value at the center of the list is used for the filtered output.
The result of applying a median filter is often similar to that of applying a mean filter, but has the major advantage of removing extreme isolated values completely, without allowing them to have an impact upon surrounding pixels. This is in contrast to a mean filter, which cannot ignore extreme pixels but rather will smooth them out into occupying larger regions (Figure 9). However, a disadvantage of a median filter is that it can seem to introduce patterns or textures that were not present in the original image, at least whenever the size of the filter increases (see Figure 13D). Another disadvantage is that large median filters tend to be slow.
Other rank filters include the minimum and maximum filters, which replace each pixel value with the minimum or maximum value in the surrounding neighborhood respectively (Figure 10). They will become more important when we discuss Binary images.
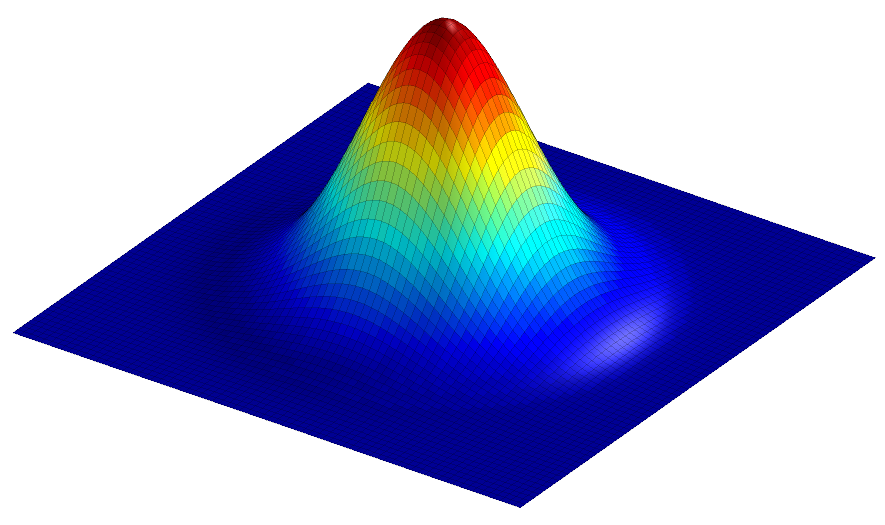
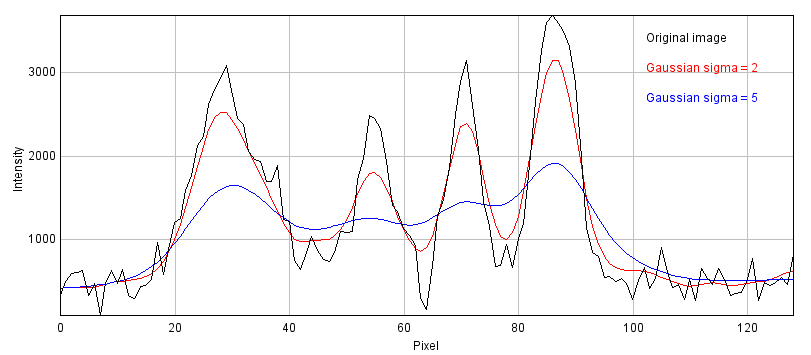
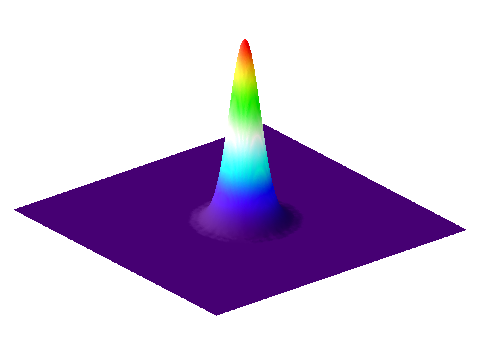
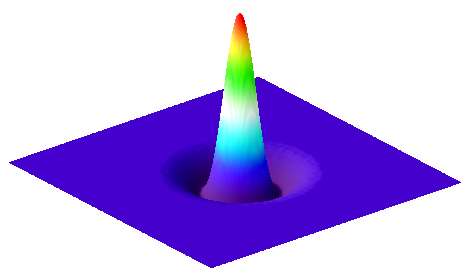
Gaussian filters
Gaussian filters from Gaussian functions
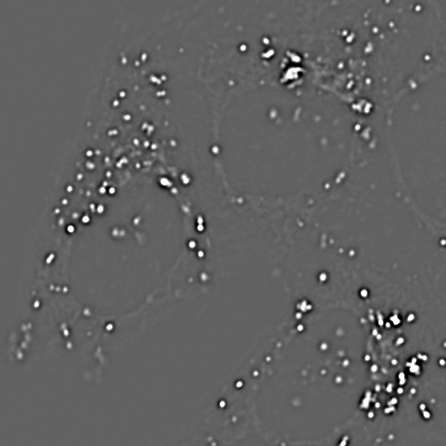
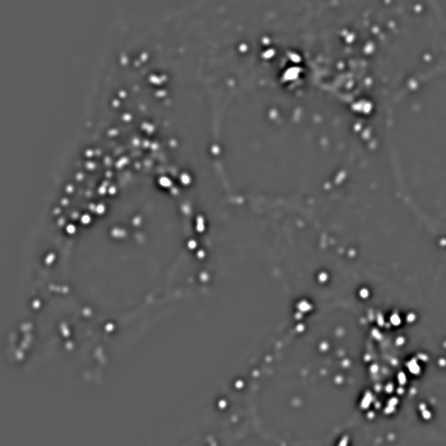
We end this chapter with one fantastically important linear filter, and some variants based upon it. A Gaussian filter is a linear filter that also smooths an image and reduces noise. However, unlike a mean filter – for which even the furthest away pixels in the neighborhood influence the result by the same amount as the closest pixels – the smoothing of a Gaussian filter is weighted so that the influence of a pixel decreases with its distance from the filter center. This tends to give a better result in many cases (Figure 11).
The coefficients of a Gaussian filter are determined from a Gaussian
function (Figure 12), and its size is controlled by a
value – so when working with ImageJ’s
Gaussian Blur… command, you will need to specify this rather than
the filter radius. is equivalent to the standard
deviation of a normal (i.e. Gaussian) distribution.
A comparison of several filters is shown in Figure 13.
Filters of varying sizes
Gaussian filters have useful properties that make them generally preferable to mean filters, some of which will be mentioned in Blur & the PSF (others require a trip into Fourier space, beyond the scope of this book). Therefore if in doubt regarding which filter to use for smoothing, Gaussian is likely to be the safer choice. Nevertheless, your decisions are not at an end since the size of the filter still needs to be chosen.
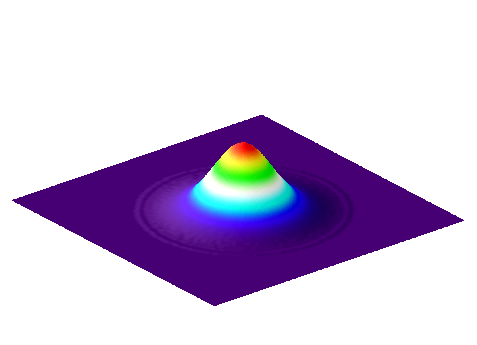
A small filter will mostly suppress noise, because noise masquerades as tiny fluorescence fluctuations at individual pixels. As the filter size increases, Gaussian filtering starts to suppress larger structures occupying multiple pixels – reducing their intensities and increasing their sizes, until eventually they would be smoothed into surrounding regions (Figure 14). By varying the filter size, we can then decide the scale at which the processing and analysis should happen.
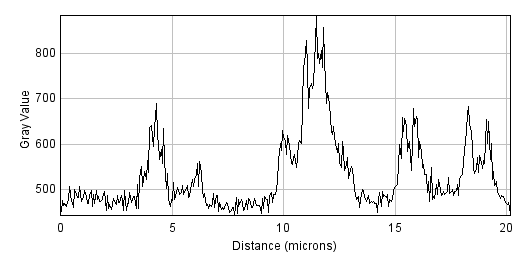
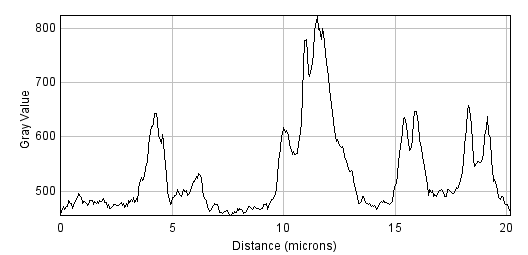
Figure 15 shows an example of when this is useful. Here, gradient magnitude images are computed similar to that in Figure 5, but because the original image is now noisy the initial result is not very useful – with even strong edges being buried amid noise (B). Applying a small Gaussian filter prior to computing the gradient magnitude gives much better results (C), but if we only wanted the very strongest edges then a larger filter would be better (D).
Difference of Gaussians filtering
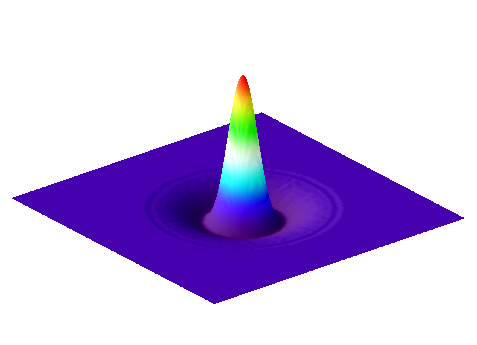
So Gaussian filters can be chosen to suppress small structures. But what if we also wish to suppress large structures – so that we can concentrate on detecting or measuring structures with sizes inside a particular range?
We already have the pieces necessary to construct one solution. Suppose we apply one Gaussian filter to reduce small structures. Then we apply a second Gaussian filter, bigger than the first, to a duplicate of the image. This will remove even more structures, while still preserving the largest features in the image. But if we finally subtract this second filtered image from the first, we are left with an image that contains the information that 'falls between' the two smoothing scales we used. This process is called difference of Gaussians (DoG) filtering, and it is especially useful for detecting small spots or as an alternative to the gradient magnitude for enhancing edges (Figure 16).
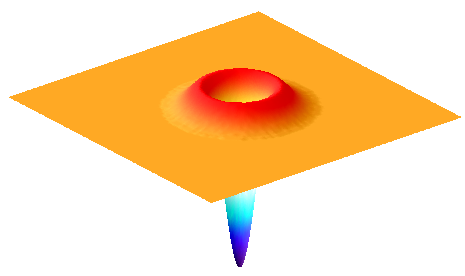
Laplacian of Gaussian filtering
One minor complication with DoG filtering is the need to select two different values of . A similar operation, which requires only a single and a single filter, is Laplacian of Gaussian (LoG) filtering. The appearance of a LoG filter is like an upside-down DoG filter (Figure 18), but if the resulting filtered image is inverted then the results are comparable[4]. You can test out LoG filtering in Fiji using [5].
Unsharp masking
Finally, a related technique widely-used to enhance the visibility of details in images – although not advisable for quantitative analysis – is unsharp masking ().
This uses a Gaussian filter first to blur the edges of an image, and then subtracts it from the original. But rather than stop there, the subtracted image is multiplied by some weighting factor and added back to the original. This gives an image that looks much the same as the original, but with edges sharpened by an amount dependent upon the chosen weight.
Unsharp masking can improve the visual appearance of an image, but it is important to remember that it modifies the image content in a way that might well be considered suspicious in scientific circles. Therefore, if you apply unsharp masking to any image you intend to share with the world you should have a good justification and certainly admit what you have done. If you want a more theoretically justified method to improve image sharpness, it may be worth looking into '(maximum likelihood) deconvolution' algorithms.