-
Measurements in fluorescence microscopy are affected by blur
-
Blur acts as a convolution with the microscope’s PSF
-
The size of the PSF depends on the microscope type, light wavelength & objective lens NA, and is on the order of hundreds of nm
-
In the focal plane, the PSF is an Airy pattern
-
Spatial resolution is a measure of how close structures can be distinguished. It is better in xy than along the z dimension.
Blur & the PSF
Introduction
Microscopy images normally look blurry because light originating from one point in the sample is not all detected at a single pixel: usually it is detected over several pixels and z-slices. This is not simply because we cannot use perfect lenses; rather, it is caused by a fundamental limit imposed by the nature of light. The end result is as if the light that we detect is redistributed slightly throughout our data (Figure 1).
This is important for three reasons:
-
Blur affects the apparent size of structures
-
Blur affects the apparent intensities (i.e. brightnesses) of structures
-
Blur (sometimes) affects the apparent number of structures
Therefore, almost every measurement we might want to make can be affected by blurring to some degree.
That is the bad news about blur. The good news is that it is rather well understood, and we can take some comfort that it is not random. In fact, the main ideas have already been described in Filters, because blurring in fluorescence microscopy is mathematically described by a convolution involving the microscope’s Point Spread Function (PSF). In other words, the PSF acts like a linear filter applied to the perfect, sharp data we would like but can never directly acquire.
Previously, we saw how smoothing (e.g. mean or Gaussian) filters could helpfully reduce noise, but as the filter size increased we would lose more and more detail. At that time, we could choose the size and shapes of filters ourselves, changing them arbitrarily by modifying coefficients to get the noise-reduction vs. lost-detail balance we liked best. But the microscope’s blurring differs in at least two important ways. Firstly, it is effectively applied to our data before noise gets involved, so offers no noise-reduction benefits. Secondly, because it occurs before we ever set our eyes on our images, the size and shape of the filter (i.e. the PSF) used are only indirectly (and in a very limited way) under our control. It would therefore be much nicer just to dispense with the blurring completely since it offers no real help, but unfortunately light conspires to make this not an option and we just need to cope with it.
The purpose of this chapter is to offer a practical introduction to why the blurring occurs, what a widefield microscope’s PSF looks like, and why all this matters. Detailed optics and threatening integrals are not included, although several equations make appearances. Fortunately for the mathematically unenthusiastic, these are both short and useful.
Blur & convolution
As stated above, the fundamental cause of blur is that light originating from an infinitesimally small point cannot then be detected at a similar point, no matter how great our lenses are. Rather, it ends up being focused to some larger volume known as the PSF, which has a minimum size dependent upon both the light’s wavelength and the lens being used.
This becomes more practically relevant if we consider that any fluorescing sample can be viewed as composed of many similar, exceedingly small light-emitting points – you may think of the fluorophores. Our image would ideally then include individual points too, digitized into pixels with values proportional to the emitted light. But what we get instead is an image in which every point has been replaced by its PSF, scaled according to the point’s brightness. Where these PSFs overlap, the detected light intensities are simply added together. Exactly how bad this looks depends upon the size of the PSF (Figure 2).
The chapter on Filters gave one description of convolution as replacing each pixel in an image with a scaled filter – which is just the same process. Therefore it is no coincidence that applying a Gaussian filter to an image makes it look similarly blurry. Because every point is blurred in the same way (at least in the ideal case; extra aberrations can cause some variations), if we know the PSF then we can characterize the blur throughout the entire image – and thereby make inferences about how blurring will impact upon anything we measure.
The shape of the PSF
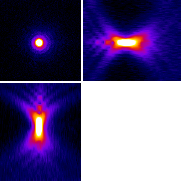
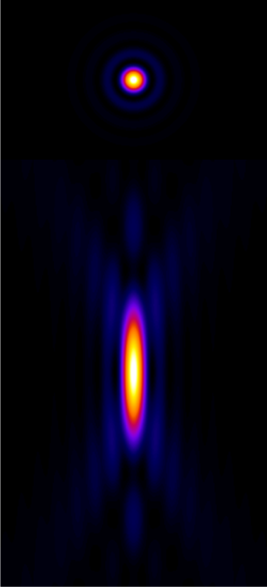
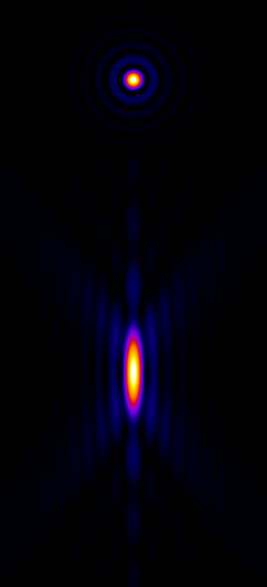
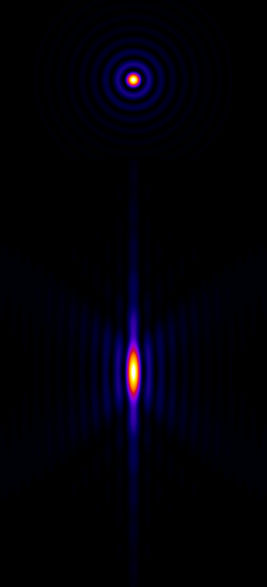
We can gain an initial impression of a microscope’s PSF by recording a z-stack of a small, fluorescent bead, which represents an ideal light-emitting point. Figure 3 shows that, for a widefield microscope, the bead appears like a bright blob when it is in focus. More curiously, when viewed from the side (xz or yz), it has a somewhat hourglass-like appearance – albeit with some extra patterns. This exact shape is well enough understood that PSFs can also be generated theoretically based upon the type of microscope and objective lenses used (C).
In & out of focus

|
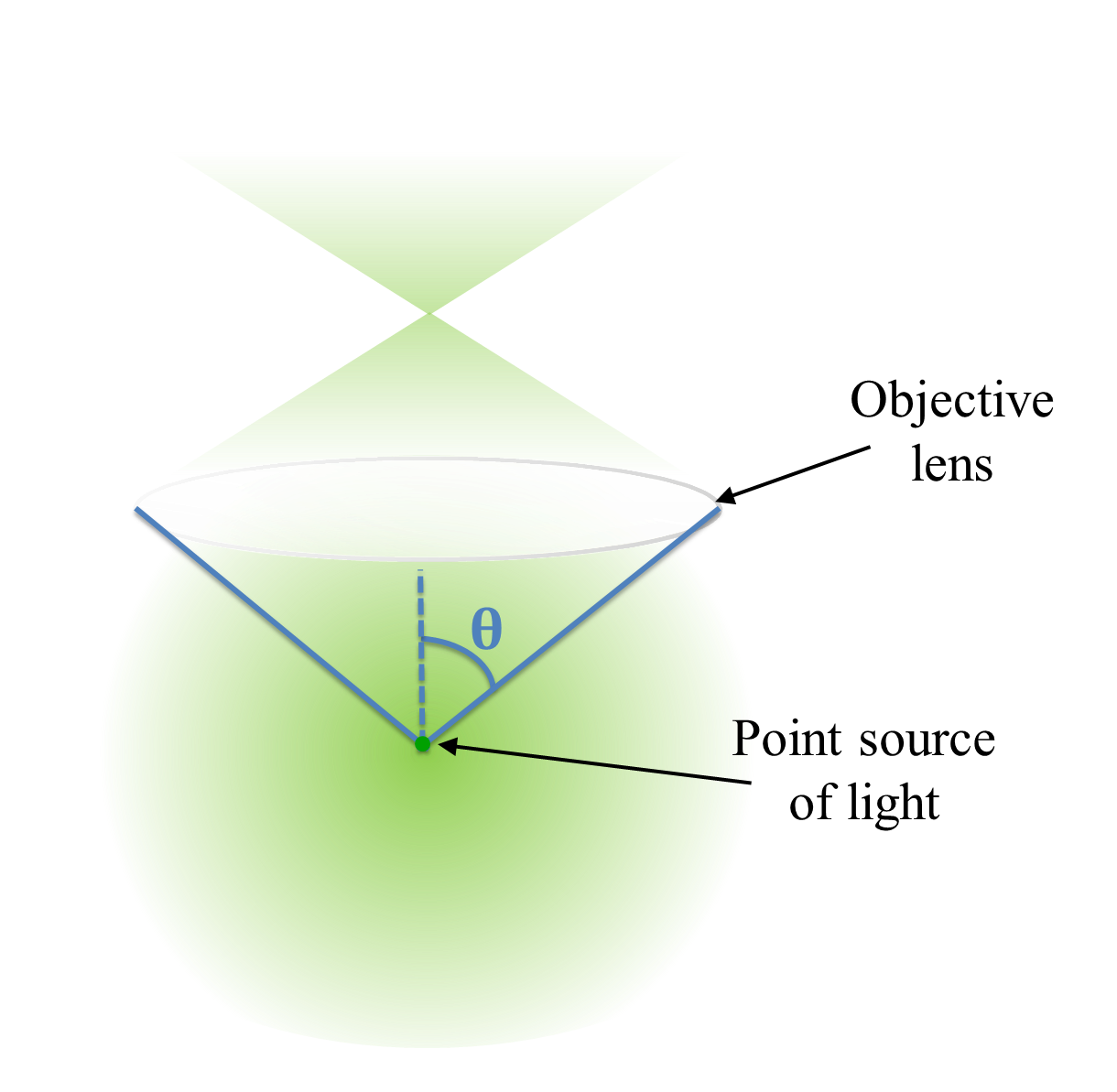
Figure 4: Simplified diagram to help visualize how a light-emitting point would be imaged using a widefield microscope. Some of the light originating from the point is captured by a lens. If you imagine the light then being directed towards a focal point, this leads to an hourglass shape. If a detector is placed close to the focal point, the spot-like image formed by the light striking the detector would be small and bright. However, if the detector were positioned above or below this focal plane, the intensity of the spot would decrease and its size would increase.
The appearance of interference
Figure 4 is quite limited in what it shows: it does not begin to explain the extra patterns of the PSF, which appear on each 2D plane as concentric rings (Figure 5), nor why the PSF does not shrink to a single point in the focal plane. These factors relate to the interference of light waves. While it is important to know that the rings occur – if only to avoid ever misinterpreting them as extra ring-like structures being really present in a sample – they have limited influence upon any analysis because the central region of the PSF is overwhelmingly brighter. Therefore for our purposes they can mostly be disregarded.
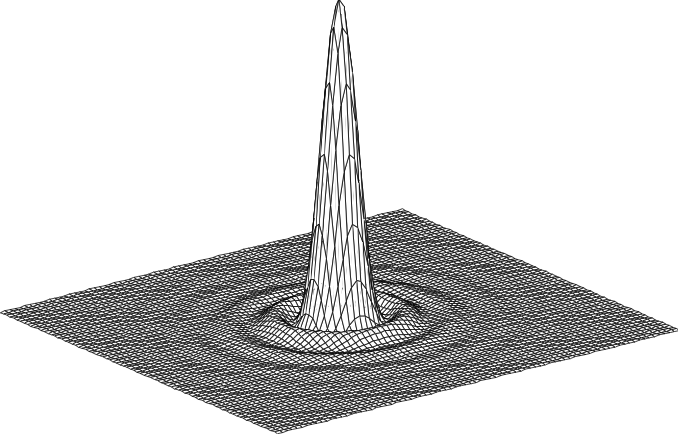
The Airy disk
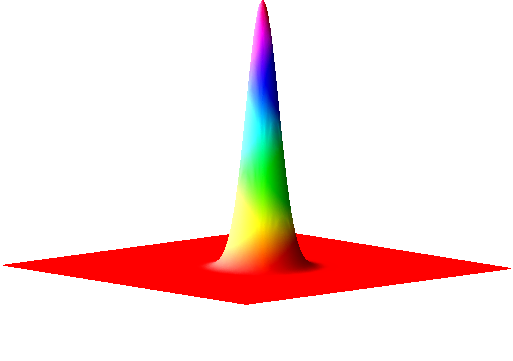
Finally for this section, the PSF in the focal plane is important enough to deserve some attention, since we tend to want to measure things where they are most in-focus. This entire xy plane, including its interfering ripples, is called an Airy pattern, while the bright central part alone is the Airy disk (Figure 6). In the best possible case, when all the light in a 2D image comes from in-focus structures, it would already have been blurred by a filter that looks like this.
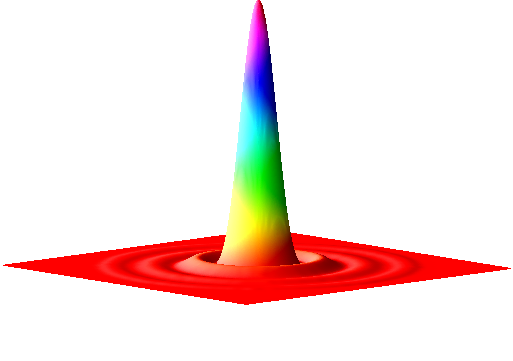
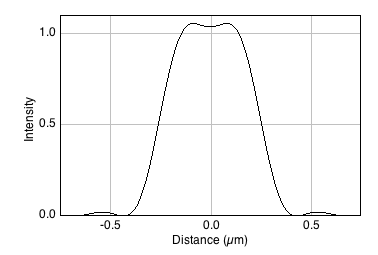
The Airy disk should look familiar. If we ignore the little interfering ripples around its edges, it can be very well approximated by a Gaussian function (Figure 7). Therefore the blur of a microscope in 2D is similar to applying a Gaussian filter, at least in the focal plane.
The size of the PSF
So much for appearances. To judge how the blurring will affect what we can see and measure, we need to know the size of the PSF – where smaller would be preferable.
The size requires some defining: the PSF actually continues indefinitely, but has extremely low intensity values when far from its center. One approach for characterizing the Airy disk size is to consider its radius as the distance from the center to the first minimum: the lowest point before the first of the outer ripples begins. This is is given by:
where is the light wavelength and NA is the numerical aperture of the objective lens[1].
A comparable measurement to between the center and first minimum along the z axis is:
where is the refractive index of the objective lens immersion medium (which is a value related to the speed of light through that medium).
Spatial resolution
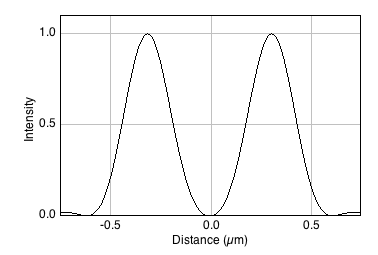
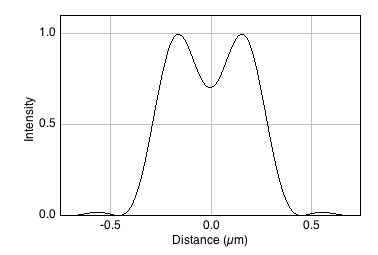
Spatial resolution is concerned with how close two structures can be while they are still distinguishable. This is a somewhat subjective and fuzzy idea, but one way to define it is by the Rayleigh Criterion, according to which two equally bright spots are said to be resolved (i.e. distinguishable) if they are separated by the distances calculated in the lateral and axial equations above. If the spots are closer than this, they are likely to be seen as one. In the in-focus plane, this is illustrated in Figure 9.
It should be kept in mind that the use of and in the Rayleigh criterion is somewhat arbitrary – and the effects of brightness differences, finite pixel sizes and noise further complicate the situation, so that in practice a greater distance may well be required for us to confidently distinguish structures. Nevertheless, the Rayleigh criterion is helpful to give some idea of the scale of distances involved, i.e. hundreds of nanometers when using visible light.
Measuring PSFs & small structures
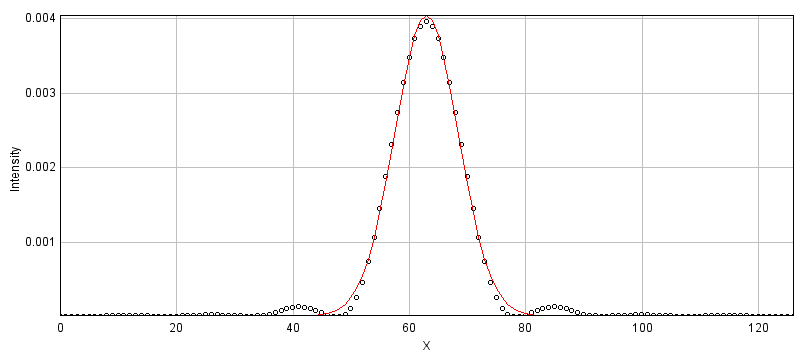
Knowing that the Airy disk resembles a Gaussian function is extremely useful, because any time we see an Airy disk we can fit a 2D Gaussian to it. The parameters of the function will then tell us the Gaussian’s center exactly, which corresponds to where the fluorescing structure really is – admittedly not with complete accuracy, but potentially still beyond the accuracy of even the pixel size (noise is the real limitation). This idea is fundamental to single-molecule localization techniques, including those in super-resolution microscopes like STORM and PALM, but requires that PSFs are sufficiently well-spaced that they do not interfere with one another and thereby ruin the fitting.
In ImageJ, we can somewhat approximate this localization by drawing a line profile across the peak of a PSF and then running . There we can fit a 1D Gaussian function, for which the equation used is
is simply a background constant, tells you the peak amplitude (i.e. the maximum value of the Gaussian with the background subtracted), and gives the location of the peak along the profile line. But potentially the most useful parameter here is , which corresponds to the value of a Gaussian filter. So if you know this value for a PSF, you can approximate the same amount of blurring with a Gaussian filter. This may come in useful in Simulating image formation.